We just had a structural report done on a house we are selling and the recommendation was to reinforce the subfloor. Here is my question. When we had the house remodeled we added cement board prior to putting tile down. Is that considered having the floor reinforced? The joist are 20 inches apart and in good condition. The inspector claims that some of the subfloor was "soft" and needed to be reinforced or replaced. To replace the subfloor we would have to tear up the new tile floor. He was not aware of the cement board or tile when he wrote the report...and he has not yet returned a call that I have placed to him. Any ideas out there. I really don't want to have to tear up the whole floor.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
reinforcing a subfloor
- Thread starter patch1239
- Start date

Help Support House Repair Talk:
This site may earn a commission from merchant affiliate
links, including eBay, Amazon, and others.
It sounds to be that he had no clue what the floor consisted of to begin with and just that the floor joists were 20" OC.
I can tell you why he's not returning your call.....Nothing like looking like a douche and an ignorant one at that when you write an official report.
Time to have someone else look at your floor.
I can tell you why he's not returning your call.....Nothing like looking like a douche and an ignorant one at that when you write an official report.
Time to have someone else look at your floor.
I am planning on installing carpet on my third floor. I will need to put something down to raise the carpet to the level that the wood floors were at. The thing that I would like to fix in the process is that the floors shake some if you walk a little heavy on it. Little things will shake on the other side of the room. It is more of an annoyance than anything serious. I guess my question is would laying another layer of plywood help stiffen it up, or is it a lot more complicated to fix?
Regards,
Regards,
travelover
Well-Known Member
- Joined
- Aug 4, 2007
- Messages
- 693
- Reaction score
- 2
I am planning on installing carpet on my third floor. I will need to put something down to raise the carpet to the level that the wood floors were at. The thing that I would like to fix in the process is that the floors shake some if you walk a little heavy on it. Little things will shake on the other side of the room. It is more of an annoyance than anything serious. I guess my question is would laying another layer of plywood help stiffen it up, or is it a lot more complicated to fix?
Regards,
It is generally best to start a new topic for your own question, but I'll reply here as this pertains to the OP's question too.
Bending strength comes from thickness. That is why a floor joist is laid so the wide part is vertical and supports the weight. The best way to make a strong floor is to use a wider board in the original construction i.e a 2x10 vs a 2 x8. Once the floor is constructed, the best way to reinforce the floor is from underneath by "sistering" a second board to the side of the existing floor joist. The maximum stress is in the center, so the sister does not have to match the joist from end to end, but must be firmly attached (glued and screwed).
A second technique is to attach each floor joist to the one next to it, so the load is shared. This is done with blocking (a perpendicular board of same width as joist attached at each end to joists) or diagonal braces which connect the bottom of one joist to the top of the adjoining joint.
Adding a layer of plywood will make the floor a little stiffer, but this will not be nearly as effective as the above two techniques.
Google "reinforcing floor joists" for more suggestions
What to do about bouncy floors
Actually, you can add as much stiffness to a floor by laying a thickness of plywood across the floor too. You should adequately attach it with screws and glue into the joists. Roughly, a 3/4 plywood panel(Not OSB!!) on the floor is equal to adding 2" in joist depth if you can stand the added height of the floor.
Patch, the cement board is not structural, only dead weight. Read this on sistering: http://www.finehomebuilding.com/PDF/Free/021184090.pdf Recommended 1-1/4" minimum plywood under c.b.u. and tile.
SuperP, here is a good one on ply layering: The design of renovations - Google Books
Craig, may I ask where you got that good information on ply/joist rating?
Be safe, Gary
SuperP, here is a good one on ply layering: The design of renovations - Google Books
Craig, may I ask where you got that good information on ply/joist rating?
Be safe, Gary
How the he@% does he know the sub floor is soft under hardy board and tile? If theres that much flex in the floor, your tiles would be popping up all over! Did you do the floor after he gave his report?
That was my exact thought and that is why I said what I did.
Nestor_Kelebay
Emperor Penguin
- Joined
- Mar 28, 2009
- Messages
- 1,844
- Reaction score
- 5
I don't really understand why people suggest "sistering" joists. I graduated from university with a Bachelor's degree in Mechanical Engineering and the design of beams is part of the course work that every mechanical and civil engineering student takes.
Instead of sistering floor joists, I'd suggest that you talk to any architectural or structural engineering firm about ADDING wood to the bottoms of your existing joists.
If you can use a glue that forms a bond that's as strong or stronger than the wood the joist is made of, then you can ADD wood to the bottom of a joist to make it stronger. That is, you can turn a 2X8 into a 2X10, or a 2X8 into a 2X12 for that matter. All that is necessary is that the glue you use and the wood you add be as strong or stronger than the wood you have now.
If you were to use a construction adhesive like LePage's PL Premium to glue and screw two pieces of fir 1X2 together (side to side), and once the glue sets up you were to take the screws out and bend that 2X2 beam until it breaks (by using a car jack, for example, to apply tremendous force), and you find out that it broke in the wood, not at the glued joint, then you have proved that the glue is stronger than the wood. If the glue is stronger than the wood, and the wood you add is as strong or stronger than the wood you have, you can do nothing but strengthen the joist by adding wood to it ANYWHERE. There rest of this post will be about where you need to add it for maximum effect.
Travelover was correct in saying that the height of the joist is one of the most important considerations to the rigidity of a joist, and he was correct, but the length of the joist is equally important. Apart from changing the cross section of the joist to make it look more like an I beam than a rectangle, or changing the material the joist is made of (magically changing the wood into steel, say), the height of the joist and the span of the beam are equally important in determining how much a beam deflects under any given load.
This web page gives the basic formulas for determining the deflections of beams:
Deflection of beams
For a solid rectangular beam like a floor joist, the ends of the beam are supported at both ends. Neglecting gravity, the joist will deflect the same amount if it's supported from below and a weight is rested on it, or if it's prevented from moving upward, and a vertical upward force is applied to it:
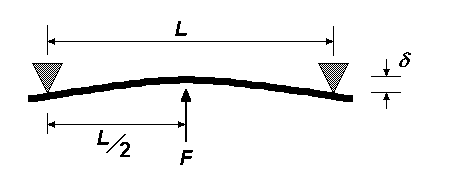
In the above drawing, the gray triangles are the supports and are assumed not to move. A force is applied at the center of the beam and the deflection of the beam is calculated as:
deflection = F*L*L*L / 48*EI
where
F is the force applied
L is the span of the beam, which is the distance between supports
E is the "Modulus of Elasticity" of the material the beam is made of. This parameter takes into account that a fir joist will bend less than a spruce joist, and one made of solid steel will bend even less. This web page gives the values of E to be used for Southern Yellow Pine, Douglas Fir, Hemlock and Spruce for various grades of these woods. For steel, use E = 30 million psi. Steel is about 15 to 20 times as stiff as wood. So, just be aware that the Modulus of Elasticity, "E" is the parameter that accounts for the strength of the material the beam is made of, and the value of E won't change unless you replace the joist or beam with one made from a different material.
http://www.southernpine.com/speciescomparisons2x6.shtml
I is the Moment of Inertia of the beam, which takes into account it's cross sectional shape. This parameter takes into account that a round solid steel bar will be stronger and bend less than a hollow steel tube of the same diameter, or that a square hollow tube will be stronger and bend less than a round hollow tube of the same height. The mathematics in the equations developed to predict beam deflection presume that the beam is a bundle of fibers. When the beam bends, those equations predict that the fibers on the top and bottom of the beam will be in compression and tension, and the fibers in the middle of the beam won't have any stress on them at all. Consequently, it's the material that's furthest away from the middle of the beam that's in the most tension and most compression and helps the most in resisting any bending of the beam. This is exactly why an I beam (with it's top and bottom flanges) is very much stronger than the same beam with those top and bottom flanges removed. And, it's also why the same 2X12 can be used as either a very rigid floor joist or a very bouncy diving board depending entirely on it's orientation relative to the applied force. So, just be aware that the Moment of Inertia, "I" is the parameter that accounts for the shape of the beam relative to the applied force.
For a solid rectangular beam (like a joist), I is calculated from the formula:
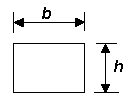
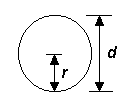
For a round beam, like a round pry bar, I is calculated from the formula:
So, just for argument's sake, let's plug the formula for I for a rectangular beam into the formula for a beam's deflection under a concentrated load at mid-span of the beam:
We have:
deflection = F*L*L*L / 48*EI
substituting I = b*h*h*h / 12, we get
deflection = 12*F*L*L*L / 48*E*b*h*h*h
or, deflection = F*L*L*L / 4*E*b*h*h*h
Now, if you sister the joists, all you're doing is effectively doubling the width of the beam, b. The result, predictable from the formula above and from common sense, is that the deflection of the sistered beam will be half of what a single beam is under any given load.
But, if you start playing with the h (height) of the beam, or the L (span of the beam), then you get much greater changes in the rigidity and deflection cuz these terms are CUBED in the formula for deflection.
So, for example, if you were to cut a hole in the basement floor, pour a reinforced concrete footing, and sit a jack post on it to support a beam supporting the floor joists in the middle of their spans, you'd effectively cut the span, L, in half. The result would be that the floor deflection would be 1/2 cubed, or 1/8 of what it was before.
Similarily, if you doubled the height of the joists, h, you'd also get 1/8 of the deflection you had before.
If, for example, you used PL Premium to glue and screw some fir strips 2 inches high by 1 1/2 inches wide to the bottoms of 2X10 floor joists, then the reduction in the deflection in the floor would be:
(9 1/2 * 9 1/2 * 9 1/2) / (11 1/2 * 11 1/2 * 11 1/2) or (9.5 cubed)/(11.5 cubed)
or 0.56, or you'd have only 56 percent of the deflection you had with the 2X10's.
That is, by adding 2 inches of wood to the bottoms of 2X10 floor joists, the deflection of the floor is 56 percent of what it was before, or approximately the same amount as if you'd used vastly more wood to sister each joist. And, strengthening the joists by adding wood to them completely avoids all of the potential additional work involved in running electrical wires and such through the sistered joists.
Aslo, that above estimate of reducing the deflection of the floor by 56 percent is based on turning the 2X10s into 2X12's. You COULD glue 2X4's edge-to-edge to the bottoms of the joists for a much larger increase in rigidity, or even glue them on to make the bottoms of the joists resemble the bottom half of an I beam (which would allow you to use shorter screws. Both of those gameplans would result in an even larger increase in rigidity of the joists, and therefore less deflection of the floor.
But, the above is not really strengthening the subfloor, as the post is entitled. It's strengthening the floor joists that support the subfloor. It could be that the inspector was saying that there's too much flexing of the subfloor between the joists. In that case, strengthening the joists won't address the problem he's complaining about. AND, it's based entirely on the assumption that you can find a glue that'll form a bond that's as strong or stronger than the wood you're gluing to. I really don't know whether PL Premium is, but it'd be an easy matter to test it.
Instead of sistering floor joists, I'd suggest that you talk to any architectural or structural engineering firm about ADDING wood to the bottoms of your existing joists.
If you can use a glue that forms a bond that's as strong or stronger than the wood the joist is made of, then you can ADD wood to the bottom of a joist to make it stronger. That is, you can turn a 2X8 into a 2X10, or a 2X8 into a 2X12 for that matter. All that is necessary is that the glue you use and the wood you add be as strong or stronger than the wood you have now.
If you were to use a construction adhesive like LePage's PL Premium to glue and screw two pieces of fir 1X2 together (side to side), and once the glue sets up you were to take the screws out and bend that 2X2 beam until it breaks (by using a car jack, for example, to apply tremendous force), and you find out that it broke in the wood, not at the glued joint, then you have proved that the glue is stronger than the wood. If the glue is stronger than the wood, and the wood you add is as strong or stronger than the wood you have, you can do nothing but strengthen the joist by adding wood to it ANYWHERE. There rest of this post will be about where you need to add it for maximum effect.
Travelover was correct in saying that the height of the joist is one of the most important considerations to the rigidity of a joist, and he was correct, but the length of the joist is equally important. Apart from changing the cross section of the joist to make it look more like an I beam than a rectangle, or changing the material the joist is made of (magically changing the wood into steel, say), the height of the joist and the span of the beam are equally important in determining how much a beam deflects under any given load.
This web page gives the basic formulas for determining the deflections of beams:
Deflection of beams
For a solid rectangular beam like a floor joist, the ends of the beam are supported at both ends. Neglecting gravity, the joist will deflect the same amount if it's supported from below and a weight is rested on it, or if it's prevented from moving upward, and a vertical upward force is applied to it:

In the above drawing, the gray triangles are the supports and are assumed not to move. A force is applied at the center of the beam and the deflection of the beam is calculated as:
deflection = F*L*L*L / 48*EI
where
F is the force applied
L is the span of the beam, which is the distance between supports
E is the "Modulus of Elasticity" of the material the beam is made of. This parameter takes into account that a fir joist will bend less than a spruce joist, and one made of solid steel will bend even less. This web page gives the values of E to be used for Southern Yellow Pine, Douglas Fir, Hemlock and Spruce for various grades of these woods. For steel, use E = 30 million psi. Steel is about 15 to 20 times as stiff as wood. So, just be aware that the Modulus of Elasticity, "E" is the parameter that accounts for the strength of the material the beam is made of, and the value of E won't change unless you replace the joist or beam with one made from a different material.
http://www.southernpine.com/speciescomparisons2x6.shtml
I is the Moment of Inertia of the beam, which takes into account it's cross sectional shape. This parameter takes into account that a round solid steel bar will be stronger and bend less than a hollow steel tube of the same diameter, or that a square hollow tube will be stronger and bend less than a round hollow tube of the same height. The mathematics in the equations developed to predict beam deflection presume that the beam is a bundle of fibers. When the beam bends, those equations predict that the fibers on the top and bottom of the beam will be in compression and tension, and the fibers in the middle of the beam won't have any stress on them at all. Consequently, it's the material that's furthest away from the middle of the beam that's in the most tension and most compression and helps the most in resisting any bending of the beam. This is exactly why an I beam (with it's top and bottom flanges) is very much stronger than the same beam with those top and bottom flanges removed. And, it's also why the same 2X12 can be used as either a very rigid floor joist or a very bouncy diving board depending entirely on it's orientation relative to the applied force. So, just be aware that the Moment of Inertia, "I" is the parameter that accounts for the shape of the beam relative to the applied force.
For a solid rectangular beam (like a joist), I is calculated from the formula:

For a round beam, like a round pry bar, I is calculated from the formula:

So, just for argument's sake, let's plug the formula for I for a rectangular beam into the formula for a beam's deflection under a concentrated load at mid-span of the beam:
We have:
deflection = F*L*L*L / 48*EI
substituting I = b*h*h*h / 12, we get
deflection = 12*F*L*L*L / 48*E*b*h*h*h
or, deflection = F*L*L*L / 4*E*b*h*h*h
Now, if you sister the joists, all you're doing is effectively doubling the width of the beam, b. The result, predictable from the formula above and from common sense, is that the deflection of the sistered beam will be half of what a single beam is under any given load.
But, if you start playing with the h (height) of the beam, or the L (span of the beam), then you get much greater changes in the rigidity and deflection cuz these terms are CUBED in the formula for deflection.
So, for example, if you were to cut a hole in the basement floor, pour a reinforced concrete footing, and sit a jack post on it to support a beam supporting the floor joists in the middle of their spans, you'd effectively cut the span, L, in half. The result would be that the floor deflection would be 1/2 cubed, or 1/8 of what it was before.
Similarily, if you doubled the height of the joists, h, you'd also get 1/8 of the deflection you had before.
If, for example, you used PL Premium to glue and screw some fir strips 2 inches high by 1 1/2 inches wide to the bottoms of 2X10 floor joists, then the reduction in the deflection in the floor would be:
(9 1/2 * 9 1/2 * 9 1/2) / (11 1/2 * 11 1/2 * 11 1/2) or (9.5 cubed)/(11.5 cubed)
or 0.56, or you'd have only 56 percent of the deflection you had with the 2X10's.
That is, by adding 2 inches of wood to the bottoms of 2X10 floor joists, the deflection of the floor is 56 percent of what it was before, or approximately the same amount as if you'd used vastly more wood to sister each joist. And, strengthening the joists by adding wood to them completely avoids all of the potential additional work involved in running electrical wires and such through the sistered joists.
Aslo, that above estimate of reducing the deflection of the floor by 56 percent is based on turning the 2X10s into 2X12's. You COULD glue 2X4's edge-to-edge to the bottoms of the joists for a much larger increase in rigidity, or even glue them on to make the bottoms of the joists resemble the bottom half of an I beam (which would allow you to use shorter screws. Both of those gameplans would result in an even larger increase in rigidity of the joists, and therefore less deflection of the floor.
But, the above is not really strengthening the subfloor, as the post is entitled. It's strengthening the floor joists that support the subfloor. It could be that the inspector was saying that there's too much flexing of the subfloor between the joists. In that case, strengthening the joists won't address the problem he's complaining about. AND, it's based entirely on the assumption that you can find a glue that'll form a bond that's as strong or stronger than the wood you're gluing to. I really don't know whether PL Premium is, but it'd be an easy matter to test it.
Last edited:
The glue and screw method though ideal from green train of thought is many times not even close to ideal.
It's great when it works.
The ideal thing abpout sistering joists is that you lose no ceiling height from below and since this method is used primarily at basement level where it is an ideal method in many of our old houses here. If you add another 2" you might be smacking your head every 16" or every step you take as you walk to your dryer.
When most people sister joists they don't glue as well. They slap a joist up there and screw it together. Quick and easy. Poor installation technique!!!
The glue and screw method is not quick. The old joists have to be prepped. Yes they have to be sanded without any dips and dives. Most old houses have joists that are rough cut. This rough cut surely won't cut the mustard.
New joists in more modern construstion need to be sanded as well yet not as aggressively.
If we are talking fir joists like in many houses you can almost pick any glue to form the wood to wood bond. Be careful in the northeast here. Many many houses were constructed with spruce yet most contractors think it's fir because they have no clue about wood usage history. Spruce for it's weight dry is extremely strong.
Nestor, great post above!!!
It's great when it works.
The ideal thing abpout sistering joists is that you lose no ceiling height from below and since this method is used primarily at basement level where it is an ideal method in many of our old houses here. If you add another 2" you might be smacking your head every 16" or every step you take as you walk to your dryer.
When most people sister joists they don't glue as well. They slap a joist up there and screw it together. Quick and easy. Poor installation technique!!!
The glue and screw method is not quick. The old joists have to be prepped. Yes they have to be sanded without any dips and dives. Most old houses have joists that are rough cut. This rough cut surely won't cut the mustard.
New joists in more modern construstion need to be sanded as well yet not as aggressively.
If we are talking fir joists like in many houses you can almost pick any glue to form the wood to wood bond. Be careful in the northeast here. Many many houses were constructed with spruce yet most contractors think it's fir because they have no clue about wood usage history. Spruce for it's weight dry is extremely strong.
Nestor, great post above!!!
Nestor... I agree but you forget to mention that applying "flanges" to the 2X10 beam actually strengthens it more because of the AD**2 property-- the area of the flange time the distance from the neutral axis squared -- trying to make it act like a efficient wideflange beam as much as possible. My example uses this by including the subflooring and some of the "flange" area. This way you can get the effect of adding two inches to the depth of the beam without decreasing headroom on the floor below.
travelover
Well-Known Member
- Joined
- Aug 4, 2007
- Messages
- 693
- Reaction score
- 2
I've got a degree in mechanical engineering, too, so I understand the physics involved. I remember working out these formulas long hand pre-calculator. 
But realistically, the OP only wanted to slap down another layer on the top side. Sistering is not ideal from an efficiency standpoint but if you are trying to keep the same ceiling height, it is a cheap, low tech way to reinforce the floor. Ditto with blocking or diagonal braces between joints.
And yes, the length of the joists is more important than the depth, but I didn't think the OP was gonna make the room smaller, and I didn't see a willingness to add posts underneath.
But realistically, the OP only wanted to slap down another layer on the top side. Sistering is not ideal from an efficiency standpoint but if you are trying to keep the same ceiling height, it is a cheap, low tech way to reinforce the floor. Ditto with blocking or diagonal braces between joints.
And yes, the length of the joists is more important than the depth, but I didn't think the OP was gonna make the room smaller, and I didn't see a willingness to add posts underneath.
Nestor_Kelebay
Emperor Penguin
- Joined
- Mar 28, 2009
- Messages
- 1,844
- Reaction score
- 5
I took engineering years ago, but I still remember and understand the basics of beam design, just as others in here do.
I just figured I'd bring out the point about strengthening the joists themselves. I always hear about people sistering joists, and there's no doubt that sistering joists will result in a stronger joist system. But, it's also true that there are other options available that may work better that haven't been presented to the homeowner.
When I have suggested these options on other Q&A forums I've posted on, I've gotten a lot of resistance. Most of the time the arguments against it went as follows "I've been doing this kinda work for 600 years, and I've never ever heard of anything so stupid in my life until you opened your mouth. Do you realize that I had to grit my teeth to stop myself from laughing out loud at what you said! That's cuz it was so mind-bogglingly stupid. Do you hear me?"
So, what do I do with criticism like that? I can explain the equations, and why adding wood should work, but I can't change prejudice, and this guy has already decided it's a stupid idea before he's even taken the time to think it through. So, I just throw the idea out there with the formulas to show why it should work, take the criticism on the chin and carry on. What else would anyone do?
I just thought I'd explain the basics so that people in here can see for themselves that there are alternatives to sistering joists that they might want to explore. If they do, then I'd recommend they proceed with the assistance of a consulting engineering firm or architectural firm to ensure that what's done is structurally sound and approved for insurance purposes. Your house is your biggest investment, and you should proceed with structural changes only with an engineering or architectural firm on side to approve the changes just to cover your A$$.
I just figured I'd bring out the point about strengthening the joists themselves. I always hear about people sistering joists, and there's no doubt that sistering joists will result in a stronger joist system. But, it's also true that there are other options available that may work better that haven't been presented to the homeowner.
When I have suggested these options on other Q&A forums I've posted on, I've gotten a lot of resistance. Most of the time the arguments against it went as follows "I've been doing this kinda work for 600 years, and I've never ever heard of anything so stupid in my life until you opened your mouth. Do you realize that I had to grit my teeth to stop myself from laughing out loud at what you said! That's cuz it was so mind-bogglingly stupid. Do you hear me?"
So, what do I do with criticism like that? I can explain the equations, and why adding wood should work, but I can't change prejudice, and this guy has already decided it's a stupid idea before he's even taken the time to think it through. So, I just throw the idea out there with the formulas to show why it should work, take the criticism on the chin and carry on. What else would anyone do?
I just thought I'd explain the basics so that people in here can see for themselves that there are alternatives to sistering joists that they might want to explore. If they do, then I'd recommend they proceed with the assistance of a consulting engineering firm or architectural firm to ensure that what's done is structurally sound and approved for insurance purposes. Your house is your biggest investment, and you should proceed with structural changes only with an engineering or architectural firm on side to approve the changes just to cover your A$$.
Last edited:
Nestor_Kelebay
Emperor Penguin
- Joined
- Mar 28, 2009
- Messages
- 1,844
- Reaction score
- 5
PS:
I think I still have a post I wrote up years ago that explains these beam equations in more detail. I don't want to hijack this thread, but am willing to post it here or in a new thread if anyone wants to read it.
I think I still have a post I wrote up years ago that explains these beam equations in more detail. I don't want to hijack this thread, but am willing to post it here or in a new thread if anyone wants to read it.
I realize that this thread is rather old, but here goes...
So, yes, I too studied engineering, and I recall the theory and equations. Everything the Nestor detailed looks correct, as I recall. In theory.
One issue that I am still struggling with is the transfer of load between the original beam (joist) and the new material.
Certainly, there are excellent bonding agents that can marry the new material to the existing material. That part should pose no problem.
But the theoretical handling of this problem seems to miss some of the realities of the situation.
Let's assume for simplicity sake that we intend to "sister" a 2x10 with a second 2x10. The typical approach would place one beside the other, effectively doubling the strength of the original beam. I agree with this.
The approach that Nestor spoke of would instead attach the second beam to the bottom of the first. Generally speaking, this would result in a 2x20. However, there is one major caveat - the added material will be by definition shorter than the original, and rather than bearing upon the fixed endpoints, the new material will be carried by the pre-existing joists.
The additional weight of material will probably be negligible as compared to the added strength. And I will assume that head room is not an issue in this example.
Even still: Nestor noted that the top most fibers of the beam would be in compression, and the bottom most fibers in tension. This is true in theory.
However, in my proposed scenario, the lower 2x10 sections do not bear upon the fixed endpoints. As such, the tension at the extreme lowest strand of the combined beam will be zero, at least at either end.
There will be some level of tension present at the same extreme lowest strand at the midpoint of the span.
How much tension will there be, and correspondingly, how much load will the new material actually pick up? Here is where my understanding begins to break down. My "gut" tells me that there is some triangular or trapezoidal load sharing pattern in the new material, as load is transferred across the glued interface and then across the material itself.
So, the 8x increase in strength that theory would suggest will be immediately diminished. Admittedly, I don't know exactly by how much, but I think we can all agree the the REAL increase will be less than 8 fold.
Also, since it is not really feasible to reduce headroom by attaching so much additional material, a realistic treatment of Nestor's idea would more likely add something modest, like 2 or maybe 3 inches of material height.
If we assume 2 inches added, at best, our 2x10s become 2x12s, which would be about 70% stronger? And as I noted, that 70% gets eaten into by the ACTUAL load sharing pattern. So, let us assume that the addition of 4 inches of new material (2x10s become 2x14s) will suffice to double the strength of the beams. Then the immediate question is: which is preferable - traditional sistering, or losing 4 inches of headroom for Nestor's approach?
Comments?
So, yes, I too studied engineering, and I recall the theory and equations. Everything the Nestor detailed looks correct, as I recall. In theory.
One issue that I am still struggling with is the transfer of load between the original beam (joist) and the new material.
Certainly, there are excellent bonding agents that can marry the new material to the existing material. That part should pose no problem.
But the theoretical handling of this problem seems to miss some of the realities of the situation.
Let's assume for simplicity sake that we intend to "sister" a 2x10 with a second 2x10. The typical approach would place one beside the other, effectively doubling the strength of the original beam. I agree with this.
The approach that Nestor spoke of would instead attach the second beam to the bottom of the first. Generally speaking, this would result in a 2x20. However, there is one major caveat - the added material will be by definition shorter than the original, and rather than bearing upon the fixed endpoints, the new material will be carried by the pre-existing joists.
The additional weight of material will probably be negligible as compared to the added strength. And I will assume that head room is not an issue in this example.
Even still: Nestor noted that the top most fibers of the beam would be in compression, and the bottom most fibers in tension. This is true in theory.
However, in my proposed scenario, the lower 2x10 sections do not bear upon the fixed endpoints. As such, the tension at the extreme lowest strand of the combined beam will be zero, at least at either end.
There will be some level of tension present at the same extreme lowest strand at the midpoint of the span.
How much tension will there be, and correspondingly, how much load will the new material actually pick up? Here is where my understanding begins to break down. My "gut" tells me that there is some triangular or trapezoidal load sharing pattern in the new material, as load is transferred across the glued interface and then across the material itself.
So, the 8x increase in strength that theory would suggest will be immediately diminished. Admittedly, I don't know exactly by how much, but I think we can all agree the the REAL increase will be less than 8 fold.
Also, since it is not really feasible to reduce headroom by attaching so much additional material, a realistic treatment of Nestor's idea would more likely add something modest, like 2 or maybe 3 inches of material height.
If we assume 2 inches added, at best, our 2x10s become 2x12s, which would be about 70% stronger? And as I noted, that 70% gets eaten into by the ACTUAL load sharing pattern. So, let us assume that the addition of 4 inches of new material (2x10s become 2x14s) will suffice to double the strength of the beams. Then the immediate question is: which is preferable - traditional sistering, or losing 4 inches of headroom for Nestor's approach?
Comments?
Nestor_Kelebay
Emperor Penguin
- Joined
- Mar 28, 2009
- Messages
- 1,844
- Reaction score
- 5
Rpineo:
When I did these calculations in 2nd or 3rd year mechanical, (I forget which year), using a mending plate to join two beams was a 3-part calculation:
1. First you calculated the size of the mending plate to carry the same bending stress as the original beam.
2. Then (since we never assumed a glued joing) you calculated the number of steel fasteners you needed to carry the load between the beam and the mending plate. (Assuming the shear strength of steel was 30,000 pounds per square inch, you calculated the number of square inches of steel you needed to carry the load between the first part of the beam and the mending plate, and that was also the number of square inches of steel you needed between the other end of the mending plate and the other end of the beam. Then, you divided the square inches of steel you needed by the cross sectional area of each fastener to get the number of fasteners at each end of the mending plate. Now, that'll be the minimum cross sectional area of steel we'll need to carry the load from joist to sister and back to joist; we can always use more fasteners to provide a larger safety factor.
3. Finally, you calculated the bearing strength of the holes to ensure that you weren't using too few fasteners and that the holes were going to elongate or "stretch" because of the stress applied to the side of the holes by each fastener.
Back then, we always presumed that steel beams had rivets or bolts holding them together, but the same calculation should apply to sistering a 2X8 or a 2X10. I think there's a rule of thumb somewhere for deciding how long the "mending plate" or sister joist needs to be, but you can't go wrong making it as long as practical. The weight of the sister is going to be negligible compared to the strength it's going to add.
Then, theoretically, you'd have to figure out based on the span tables how much load each joist is supposed to be supporting if the design is supposed to be 40 pounds per square foot of floor area (I seem to recall) and the joists are spaced on 16 inch centers. Of the top, that would work out to about (4/3) X 40, or about 53 pounds per lineal foot of joist span.
Now, use your beam equations to find out what the bending stress is on that joist is at the middle (or where it's broken) and divide that by 30,000 pounds per square inch shear strength of steel to find out how many square inches of steel fastener you need to carry the load between the joist and the sister, and you need that same area of steel at the other end of the sister to carry that same load back to the beam. (What we're doing here is working out how much steel we need to carry the load the original beam supported, and assuming the sister will be supporting the same amount of load, and working out based on a shear strength how many square inches of steel we need to carry that load, and then based on area, how many fasteners we need. But, in the real world, nails are cheap, and so most people would just go nutz with their nailing just to be on the safe side rather than do any calculations.)
When we did the bearing force calculations, we assumed the bolts or rivets were rigid and didn't bend, and in this calculation the equivalent assumption would be that the nails used to nail the sister to the joist are rigid and won't bend. So, you'd get the compressive strength of fir and knowing the bearing area between the nail and the wood, work out whether or not the wood will compress permanently (and therefore the holes elongate) as a result of the force applied to the wood by the nails. You know the shear force carried by each nail and you know the compressive strength of the wood, so you can determine if the wood is going to crush at each nail location... or not.
I suppose that if you treated the nail like a round beam, you could work out the force required to bend the nail, and see if that's greater or smaller than the bearing force on the holes. That'll tell you whether or not the nails will bend, and if so, ya gotta use more of them.
That's how I recall doing steel beam calculations, and I expect you'd do exactly the same thing for using a wooden mending plate to repair a wooden joist, or just to sister each of the joists in a floor. You're just working out how much steel you need to carry the load of each joist, and then ensuring that you use enough fasteners that the compressive strength of the wood isn't being exceeded. In all the calculations we ever did, we always assumed that each fastener carried the same load regardless of where it was located, and that doesn't seem reasonable to me. However, that's what we assumed in doing the calculations.
Anyhow, it's a 3 step calculation; figure out how much stress the beam or mending plate is supposed to hold, then figure out how many square inches of steel in sheer is needed to carry that load, then figure out how many fasteners you need to provide that area of steel, and check that the load on each fastener doesn't crush the hole it's in. Don't you remember doing that?
When I did these calculations in 2nd or 3rd year mechanical, (I forget which year), using a mending plate to join two beams was a 3-part calculation:
1. First you calculated the size of the mending plate to carry the same bending stress as the original beam.
2. Then (since we never assumed a glued joing) you calculated the number of steel fasteners you needed to carry the load between the beam and the mending plate. (Assuming the shear strength of steel was 30,000 pounds per square inch, you calculated the number of square inches of steel you needed to carry the load between the first part of the beam and the mending plate, and that was also the number of square inches of steel you needed between the other end of the mending plate and the other end of the beam. Then, you divided the square inches of steel you needed by the cross sectional area of each fastener to get the number of fasteners at each end of the mending plate. Now, that'll be the minimum cross sectional area of steel we'll need to carry the load from joist to sister and back to joist; we can always use more fasteners to provide a larger safety factor.
3. Finally, you calculated the bearing strength of the holes to ensure that you weren't using too few fasteners and that the holes were going to elongate or "stretch" because of the stress applied to the side of the holes by each fastener.
Back then, we always presumed that steel beams had rivets or bolts holding them together, but the same calculation should apply to sistering a 2X8 or a 2X10. I think there's a rule of thumb somewhere for deciding how long the "mending plate" or sister joist needs to be, but you can't go wrong making it as long as practical. The weight of the sister is going to be negligible compared to the strength it's going to add.
Then, theoretically, you'd have to figure out based on the span tables how much load each joist is supposed to be supporting if the design is supposed to be 40 pounds per square foot of floor area (I seem to recall) and the joists are spaced on 16 inch centers. Of the top, that would work out to about (4/3) X 40, or about 53 pounds per lineal foot of joist span.
Now, use your beam equations to find out what the bending stress is on that joist is at the middle (or where it's broken) and divide that by 30,000 pounds per square inch shear strength of steel to find out how many square inches of steel fastener you need to carry the load between the joist and the sister, and you need that same area of steel at the other end of the sister to carry that same load back to the beam. (What we're doing here is working out how much steel we need to carry the load the original beam supported, and assuming the sister will be supporting the same amount of load, and working out based on a shear strength how many square inches of steel we need to carry that load, and then based on area, how many fasteners we need. But, in the real world, nails are cheap, and so most people would just go nutz with their nailing just to be on the safe side rather than do any calculations.)
When we did the bearing force calculations, we assumed the bolts or rivets were rigid and didn't bend, and in this calculation the equivalent assumption would be that the nails used to nail the sister to the joist are rigid and won't bend. So, you'd get the compressive strength of fir and knowing the bearing area between the nail and the wood, work out whether or not the wood will compress permanently (and therefore the holes elongate) as a result of the force applied to the wood by the nails. You know the shear force carried by each nail and you know the compressive strength of the wood, so you can determine if the wood is going to crush at each nail location... or not.
I suppose that if you treated the nail like a round beam, you could work out the force required to bend the nail, and see if that's greater or smaller than the bearing force on the holes. That'll tell you whether or not the nails will bend, and if so, ya gotta use more of them.
That's how I recall doing steel beam calculations, and I expect you'd do exactly the same thing for using a wooden mending plate to repair a wooden joist, or just to sister each of the joists in a floor. You're just working out how much steel you need to carry the load of each joist, and then ensuring that you use enough fasteners that the compressive strength of the wood isn't being exceeded. In all the calculations we ever did, we always assumed that each fastener carried the same load regardless of where it was located, and that doesn't seem reasonable to me. However, that's what we assumed in doing the calculations.
Anyhow, it's a 3 step calculation; figure out how much stress the beam or mending plate is supposed to hold, then figure out how many square inches of steel in sheer is needed to carry that load, then figure out how many fasteners you need to provide that area of steel, and check that the load on each fastener doesn't crush the hole it's in. Don't you remember doing that?
Last edited:
Rpineo:
<snip>
Don't you remember doing that?
What I remember most about sizing and design calculations was that we would utilize a set of assumptions in order to reduce our "problem" to a nice, neat theoretical approximation. Then we would labor to produce pages and pages of meticulous, painstaking mathematics. We would then compare the results of these seemingly endless equations against some tables to determine the size of beam or plate or cable(s) that we would need.
And then we would multiply that requirement by a factor of 2 or 3 for "safety", because ultimately, nobody really knew if all the theory would actually work in practice!
But that aside...
If I read your post correctly, you are discussing the sizing math around the following configuration:
(1) Start with existing beam (joist). Assume a 2x10 wooden joist.
(2) Attach a second 2x? member (lets say a 2x6) along the bottom edge. This theoretically results in a 2x16 compound joist.
(3) Secure the beams together using mending plate(s) - as shown in attached sketch, where 'x' chars are mending plate(s).
My original post was meant to illustrate my uncertainty about how closely this practical application would match the theoretical effectiveness. I admit that it has been some time since I have had to do such math, so my misgivings are based mainly on gut feeling. Also, the notion of sistering joists has been around for a long, long time. So has physics. If "sistering" in this fashion was the superior approach, then one is left to wonder why nobody has been doing it this way. Is there some major practical drawback, or is Nestor really onto something here?
If the latter, you might want to consider a patent!

Nestor_Kelebay
Emperor Penguin
- Joined
- Mar 28, 2009
- Messages
- 1,844
- Reaction score
- 5
Rpineo:
I think the reason why adding wood to joists isn't commonly done is because it's only recently that we've had glues that cure to form bonds that are as strong as wood. There have been other glues that form super strong bonds, like the glues used to hold laminated airplane propellers together, but these glues aren't practical to use in the field, such as in someone's basement. Now we have moisture cure polyurethane glues (like LePage's PL Premium) that are so strong that the wood they're gluing together will break before the glued joint will. And, of course, it takes time for ANY new idea to gain acceptance simply because everyone is convinced that the way they've been doing it for years is the "right" way to do it, and all other ways are either bogus or "short cuts".
Until recently, there simply haven't been wood glues that can be applied in the field that would cure to a bond stronger than the wood. So, "sistering" joists has been the fail safe alternative. But, now we have moisture cure polyurethane glues like LePage's PL Premium that WILL cure to a bond stronger than the original wood, and that's what makes the option of "adding wood to make a bigger, stronger joist" feasible. Until now, that option hasn't been available because the glues simply didn't form strong enough bonds and contractors tend to stick with "tried and true" solutions to prevent call-backs.
And, that's pretty much the definition of progress. A better product in one technology makes an alternative and advantageous method of doing something feasible in a different technology.
I've gotten a lot of flack on the internet from even suggesting that you can make a joist stronger by adding wood to it (so long as the wood and glue used are as strong or stronger than the original wood), and anyone with an engineering background will immediately see that there's no reason why that wouldn't work THEORETICALLY at least. But, (and I think) the problem is that until recently, we simply didn't have glues that were strong enough to make this a PRACTICAL alternative, and so no one did it. And, I fell into the old trap: "If what you're saying will work, why doesn't anyone do it?" Now we have much stronger glues that can be field-applied, and you're likely going to see people strengthening floors and houses by making the existing joists "taller" rather than sistering joists.
So, I'm going to keep telling people about this alternative, but I'm also going to stress that everything hinges on there not being ANY slippage at the joint between the old wood and the new wood, and therefore a super strong glue like PL Premium has to be used, and let people make up their own minds.
We all learn from each other in here.
I think the reason why adding wood to joists isn't commonly done is because it's only recently that we've had glues that cure to form bonds that are as strong as wood. There have been other glues that form super strong bonds, like the glues used to hold laminated airplane propellers together, but these glues aren't practical to use in the field, such as in someone's basement. Now we have moisture cure polyurethane glues (like LePage's PL Premium) that are so strong that the wood they're gluing together will break before the glued joint will. And, of course, it takes time for ANY new idea to gain acceptance simply because everyone is convinced that the way they've been doing it for years is the "right" way to do it, and all other ways are either bogus or "short cuts".
Until recently, there simply haven't been wood glues that can be applied in the field that would cure to a bond stronger than the wood. So, "sistering" joists has been the fail safe alternative. But, now we have moisture cure polyurethane glues like LePage's PL Premium that WILL cure to a bond stronger than the original wood, and that's what makes the option of "adding wood to make a bigger, stronger joist" feasible. Until now, that option hasn't been available because the glues simply didn't form strong enough bonds and contractors tend to stick with "tried and true" solutions to prevent call-backs.
And, that's pretty much the definition of progress. A better product in one technology makes an alternative and advantageous method of doing something feasible in a different technology.
I've gotten a lot of flack on the internet from even suggesting that you can make a joist stronger by adding wood to it (so long as the wood and glue used are as strong or stronger than the original wood), and anyone with an engineering background will immediately see that there's no reason why that wouldn't work THEORETICALLY at least. But, (and I think) the problem is that until recently, we simply didn't have glues that were strong enough to make this a PRACTICAL alternative, and so no one did it. And, I fell into the old trap: "If what you're saying will work, why doesn't anyone do it?" Now we have much stronger glues that can be field-applied, and you're likely going to see people strengthening floors and houses by making the existing joists "taller" rather than sistering joists.
So, I'm going to keep telling people about this alternative, but I'm also going to stress that everything hinges on there not being ANY slippage at the joint between the old wood and the new wood, and therefore a super strong glue like PL Premium has to be used, and let people make up their own minds.
We all learn from each other in here.
Last edited:
With regard to "obvious" patents, see: Patently Absurd (James Gleick)
In any case, I was speaking in jest.
Thanks for your thoughtful and detailed posts on this subject. This discussion has been most enlightening. I have a few joists that still require attention - I may test your approach.
In any case, I was speaking in jest.
Thanks for your thoughtful and detailed posts on this subject. This discussion has been most enlightening. I have a few joists that still require attention - I may test your approach.



